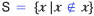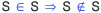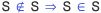불완전성 정리_쿠르트 괴델

 

오늘날 컴퓨터는 우리의 생활 전반에 영향력을 행사하고 있다. 이제 컴퓨터가 없는 현대사회란 도저히 생각할 수 없는 것이다. 인터넷의 등장, 컴퓨터의 제어 관리기능 등 현대 컴퓨터의 사용범위는 무궁무진 하다. 하지만 컴퓨터가 가진 본래의 역할은 그 이름에 고스란히 남아있다. 그것은 바로 ‘계산’ 기능이다.   도대체 이 현대 계산이론은 누가 처음으로 도입했을까? 단지 한 두 사람이 이뤄낸 성과는 아니겠지만, 학자들은 대체로 영국의 수리논리학자 앨런 튜링(Alan Turing, 1912~1954)에게 그 공을 돌린다. 그러나 조금 더 나아가 보면, 튜링은 미국의 수학자 쿠르트 괴델(Kurt Gödel, 1906~1978)의 업적과 생각을 실제 컴퓨터 설계에 확장 구현한 것이라는 학문적 사실을 확인하게 된다. 괴델과 튜링은 타임지가 선정한 지난 20세기 가장 영향력 있던 인물 100명에 든 단 2명의 수학자들이다.   두 사람은 모두 수학의 분야 중 수리논리학(수학과 논리학의 하위분야. 전산학 및 철학논리와 밀접하게 연관)에서 업적을 이뤘다는 공통점을 갖고 있다. 하지만 튜링이 괴델의 생각을 발전시켜 현대 컴퓨터 이론의 기초를 세웠다는 면에서, 우리는 괴델에 더 주목하게 되는 것이다.     가능성이 잠재돼 있던 괴델의 학창시절

쿠르트 괴델. <출처: wikipedia.org>

괴델의 업적이나 학문적 영향은 아인슈타인의 상대성 이론에 비교되곤 한다. 사실 두 사람은 그들이 머물렀던 미국 고등과학연구소를 대표하는 아이콘들이었다. 1930년대 후반의 혼란스런 정치상황에서 괴델은 오스트리아를 떠나 고등과학연구소로 영구 이주한다. 하지만 괴델은 아인슈타인에 비해 대중들에게 덜 알려져 있다. 컴퓨터가 현대사회에 미치는 영향, 인지과학의 태동 등을 볼 때 괴델의 업적이 오늘날 더욱 그 진가를 나타내고 있음에도 불구하고 이렇듯 잘 알려지지 않은 까닭은, 언뜻 그의 은둔자적 삶과도 연관이 있어 보인다.   1906년 4월 오스트리아 브르노(현 체코령)에서 태어난 괴델은 직물업계에 성공한 아버지 덕에 어린 시절을 넉넉하게 보낸 편이었다. 뭐든 질문을 잘해서 ‘왜요’ 도령(der Herr Warum: Mr. Why)으로 불린 그는 모든 과목에서 최고성적을 내는 우수하고 영민한 학생이었다. 다만 어릴 때부터 건강이 좋지 않았는데, 그는 일생 동안 스스로 읽은 의학지식을 더 신뢰하며 지나친 건강 염려증을 갖고 살았다. 이는 말년에 음식섭취를 거부해 그를 죽음에 이르게 한 원인이 되기도 했다.   1924년 오스트리아의 비엔나 대학에 입학해, 그 곳에서 십여 년간 학자로 성장하며 그의 생애 최대 업적들을 이루게 된다. 대학에서는 물리학을 시작으로 철학, 수학을 공부했는데, 지도교수 한(Hans Hahn)을 만난 이후, 그의 관심은 수리논리학에 집중된다.

 

한과 철학자 카르납 등이 주도한 비엔나 서클은 논리실증주의(과학의 논리적 분석 방법을 철학에 적용하고자 하는 사상)로 유명했는데, 괴델을 정식으로 초청했다. 괴델은 서클의 주된 의견들에 동의하진 않았다. 하지만 이 서클이 학생이었던 그가 학문대상을 설정하는 데 지적 자극제 및 안내서가 된 것은 분명하다.     수리논리학의 탄생과 발달 여기서 당시 수리논리학의 탄생과 발달을 잠시 살펴보자. 수리논리학은 수학의 기초를 건설하는 집합론, 기호논리학 등을 포괄하는 학문이란 의미에서 수학기초론으로도 불린다. 18, 19세기에 거듭된 수학의 성과는 엄밀성이 미처 확보되지 못한 상태에서 얻어졌다. 예를 들어 수열의 수렴성, 함수 연속성과 미분 가능성 등의 엄밀한 정의가 확립되지 않은 가운데 많은 결과들이 발견됐고, 때로는 모순되거나 잘못된 결과가 여과 없이 받아들여지기도 했다. 이런 난점들을 타개하고 수학의 기초를 건설하는 도구로 집합론이 거론됐다.

 

이 이론은 게오르크 칸토어(Georg Cantor, 1845~1918)가 19세기 말 우연한 계기를 통해 확립한 것으로, 초기 일부의 거부에도 불구하고 점차 받아들여진다.   어어는 집합론의 논법으로, 당시까지 미지의 영역으로 터부시 돼왔던 무한 개념을 엄밀히 다룰 수 있었다. 특히 무한집합 사이의 ‘크기’(또는 기수, cardinality)를 일대일 대응으로 논하는데, 이는 매우 획기적인 생각이었다. 예를 들어 자연수 집합은 유리수 집합의 부분집합임에도 서로 간에 일대일 대응이 존재함을 보여, 크기가 같다는 결론을 얻는다.   하지만 실수 집합과 유리수 집합 간엔 일대일 대응이 존재하지 않음도 보여, 실수 집합의 크기가 유리수 집합보다 크다는 결론을 얻는다. 칸토어는 더 나아가, ‘유리수 집합보다는 크지만 실수 집합보다는 작은 무한집합이 존재하느냐’ 질문했고, 그런 무한집합이 없을 것이라 예상했다. 이것이 유명한 그의 ‘연속체 가설’이다. 그는 남은 일생동안 이 문제에 매달리는데, 결국 해결하지 못하고 정신병동에서 쓸쓸히 죽었다고 전해진다. 이 문제는 잘 알려진 대로 후대에 괴델과 코헨에 의해 풀린다.

집합론을 확립한 게오르크 칸토어.  <출처 : wikipedia.org>

 
 

집합론의 문제점 발견, 새로운 학문 요구 한편 20세기에 접어들어 수학자들은 집합론을 통해 수학의 기초를 건설하며, 모순 없고 엄밀한 수학을 재구성 할 수 있으리라는 희망에 부풀어 있었다. 하지만 이런 기대는 ‘러셀(Bertrand Russell)의 역리’라 불리는 다음과 같은 문제가 발견되며 흔들리게 된다. 칸토어의 집합론은 특정성질을 공통으로 갖는 원소들의 집합은 항상 존재한다고 전제한다. 그렇다면 자기 자신을 원소로 갖지 않는 원소들을 모은 집합 S가 존재한다. 집합기호를 쓰면 아래와 같다.

 

‘러셀의 역리’를 발표한 버트런드 러셀.  <출처 : wikipedia.org>

즉, S는 '원소 x는 자기 자신을 원소로 갖지 않는다'는 조건을 만족하는 원소들의 집합니다. 우선 여기서 S가 S의 원소라 가정해 보자. 즉 S∈S라 하자. 그러면 집합 S는 자신 S의 원소가 돼, 성질 자기 자신을 원소로 갖지 않는다는 집합 S의 조건을 만족해야 한다. 기호로 나타내면 다음과 같다.     그렇다면 이번엔, S가 S의 원소가 아니라고 가정해 보자. 그렇다면 S는 집합 S의 조건을 만족하는 원소이므로 S에 들어간다. 즉, 아래의 결과를 유도할 수 있다.      정리하면 아래와 같은 모순된 결과를 얻는다.

 

러셀의 역리로 인해, 수학의 기초를 세우는데 모순이 생기지 않는, 수정되고 좀 더 심대한 집합론 및 수학 기초론의 등장이 요구됐다. 이 후 이러한 문제를 해결하기 위한 학파들이 등장해 각자의 주장을 펼치게 된다. 괴델이 수리논리학을 연구하고자 결심한 1920년대의 상황이 이러했던 것이다.    조금만 상상력을 동원하면, 이 시점이 서구 수리과학역사에 있어서 매우 혼란스러우면서도, 동시에 새로운 도약의 계기가 되는 시점임을 알아차릴 수 있다. 과학의 근간이 되는 수학의 세밀한 전개가 요구되던 즈음, 그 도구로 각광받던 집합론에 근본적 결함이 발견됐다. 이는 조금 과장되게 표현하면, 인류의 역사와 더불어 시작된 과학성과 전체가 송두리째 무너질 수도 있다는 위기감과 동시에, 이를 타개하기 위한 새로운 학문적 인식이 태동해야 한다는 절박감이 감돌던 시기라 말할 수 있다.

 

당시 급진적인 견해를 피력하는 부류도 있었고, 수학을 논리학에 귀속시키려는 시도도 있었다. 하지만 가장 널리 받아들여지고, 오늘날 현대 수학의 근간이 되는 정론은 힐베르트(Hibert)의 형식주의 또는 공리론적방법론이다.   이를 한마디로 설명하긴 매우 힘드나, 불완전하나마 요약해보자. 우선 인간의 언어가 가지는 결함을 제거하기 위해 모든 수학의 명제를 형식적 기호의 나열로 바꾼다. 그런 명제들 중, 모순이 생성되는 요소를 피해 수학의 공리들을 세우고, 거기서 새로운 명제를 유도하는 법칙을 세운다. 이해하기 쉽게 설명하면, 일종의 기계적 프로그램으로 수학을 이해하자는 것이다. 힐베르트는 이러한 형식적이고 기계적 체계 하에서 수학의 기본 공리를 세심히 설계하면, 모순이 절대로 유도되지 않는 것을 보일 수 있으리라 예상했다.    즉, ‘러셀의 역리’와 같은 문제가 발생하지 않는 수학의 기초가 다져지는 것을 기대한 것이다. 이것을 ‘힐베르트 프로그램’이라 부른다. 실제로 체르멜로(Zermelo)는, 요즘 체르멜로-프랭켈 공리라 불리는, 모순이 없을 것으로 예상되는 집합론의 공리들을 제안했다.

집합론의 공리를 제안한 힐베르트. <출처: wikipedia.org>

 
 

학계를 깜짝 놀라게 한 ‘불완전성 정리’ 발표 1931년, 괴델은 20대의 나이에 학계를 깜짝 놀라게 한 세기적 결과인 불완전성 정리를 발표한다. 이것이 바로 괴델을 유명하게 만든 이론이다. 이 정리의 증명 속에는 앞서 컴퓨터에서 언급한 계산이론의 토대가 담겨져 있다. 괴델의 정리는 너무나도 신비하게 들려서, 일생을 들이더라도 그것에 대해 완벽하게 이해해야겠다는 갈구가 생길 정도이다. 불완전성 정리를 한마디로 요약하긴 힘드나, 축약해본다면 ‘진리임에도 증명될 수 없는 수학적 명제가 존재한다’는 것이다. 도대체 이것이 무슨 말인가? 수학적 명제는 증명을 통해 진리임이 밝혀지는데, 증명될 수 없는 명제가 진리인 것은 어떻게 알 수 있는가? 그러면 수학적 진리란 무엇이고, 그것을 증명한다는 의미는 정확히 무엇인가? 그의 정리는 제일, 제이 불완전성 정리들로 나눠진다. 제일 불완전성 정리는 대략적으로 서술하면, 수학에서는 증명도 부정도 되지 않는 명제가 반드시 존재한다는 것이다. 사실 이것은 앞서 언급한 칸토어의 연속체 가설과 연관된다. 괴델은 연속체 가설이, 제일 불완전성 정리에서 나타나는 것처럼 증명도 부정도 안 되는 명제일 것이라 추측했다. 마침내 그는 1930년대 중반, 연속체 가설이 수학에서 ‘부정되지 않는 명제’임을 증명하는데 성공한다. 그 후 1960년대에 와 비로서 코헨(Paul J. Cohen)이란 젊은 수학자에 의해 연속체 가설이 ‘증명도 되지 않는 명제’임이 밝혀짐으로 연속체 가설 문제의 종지부가 찍힌다. 코헨은 그 업적으로 수학자 최고상이라 할 수 있는 필즈(Fields)상을 받는다.   제이 불완전성 정리는 더욱 놀랍다. 수학을 전개하는 근본 공리를 선정해 그 체계가 정말 모순이 없다면, 그 모순이 없다는 사실 자체는 (그 체계의 논리전개로는) 증명을 할 수 없다는 것이다. 이것은 앞서 언급한 힐베르트의 프로그램이 성취될 수 없다는 것을 의미한다. 수리학문계는 다시 한 번 커다란 충격과 놀라움에 휩싸인다. 괴델의 정리는 힐베르트나 그 이전 수학자들이, ‘우리가 알고자 하는 수학적 문제들은 결국 진리이거나 거짓으로 판명 또는 증명될 것이라’는 당연하다고 여겼던 믿음이 옳지 않다는 것이다. 이는 인간 인식에 근본적인 한계가 있음을 매우 분명하게 보여준 하나의 세기적 사건이었다.   제일, 제이 정리를 한마디로 요약하면, ‘진리이나 증명되지 않는 수학적 명제가 존재한다’이다. 제이 정리의 경우, 방금 살핀 것과 같이, ‘수학에 모순이 없다’는 명제 자체는 진리여야 함에도, 증명될 수 없다는 것이다. 제일 정리의 경우도, 수학에서 증명도 반증도 되지 않는 명제는, 플라톤적 관점에서 그 자신 또는 자신의 부정명제 둘 중 하나는 참일 수밖에 없으나, 어느 것도 증명되지 않는다.    괴델은 참인 수학적 명제들의 범위가, 인간이 궁극적으로 증명의 방법을 통해 참으로 확인해 인식할 수 있는 명제들의 범위를 넘어선 것을 보인 것이다. 이를 위해 우선 `인간이 참으로 인식 또는 증명할 수 있는 명제'들의 범위를 규정하기 위해 `계산 가능하다'는 개념을 최초로 제안하게 된다. 나중에 튜링과 후대 학자들에 의해 정의가 확장 보강되고, 튜링은 그렇다면 기계적 프로그램으로 `계산 가능하다는 개념'을 실행하는 장치를 만들 수 있지 않을까 생각했고, 실제 컴퓨터를 설계하기에 이른 것이다.     불완전성 정리가 미친 영향 불완전성 정리로 힐베르트의 원래 의도 했던 계획이 무산됐다고 해서 그의 형식주의가 사라진 것은 아니다. 그가 처음 제시했던 수학의 형식적 재구성에 관한 철학과 관점은 계속 유효하고 올바른 방향이라 여겨졌고, 현대수학은 그의 형식주의의 발전에 바탕을 두고 있다. 즉, 인간의 근본적 인식의 한계로 인해 힐베르트가 원하던 것을 100% 얻을 순 없다 하더라도, 그의 주장은 기본적으로 옳았다는 것이다. 따라서 불완전성 정리는 칸토어 이후 제기돼 왔던 수학 기초론의 기본 논의를 무너뜨린 것이 아니라, 오히려 문제의 본질을 드러내고 한계 속에서도 계속 작업을 해야 함을 알려 준 것이다. 따라서 이후, 대부분의 수학자들이 수학기초론의 근본적 인식에 동의하게 되는 계기를 마련해, 출렁이던 초기 수리논리학 역사가 안정되고 급속한 후속 진보를 이루는 토대가 된 것이다.   뿐만 아니라 괴델의 불완전성 정리는 분석철학, 인식론에 영향을 미치고 있으며, 언어학, 현대의 인지과학에 까지 파급력을 끼치고 있다. 논리학 내에서는 정리의 확장이, 양상논리라는 형태로 발전해 오늘에 이른다. 정리의 증명에 사용된 코딩이론, 계산가능성론 등은 후대 튜링, 폰 노이만(von Neumann) 등에 의해 발전돼, 세계 최초의 현대적 컴퓨터 설계를 위한 이론 배경이 된다.   2006년에는 괴델의 탄생 백주년을 맞아 오스트리아 비엔나 대학에서 기념학술대회가 개최됐다. 여러 분야의 학자들이 참가했으며 괴델의 우주론, 이론 컴퓨터 학에 미친 괴델의 공헌에 대한 발표가 있었다. 괴델의 업적이 신학, 철학 등의 인문학과 인지과학에 미친 영향에 대한 보고가 다음날 계속 됐다. 그의 주 연구 분야였던 집합론, 수리논리학에서 현대에도 계속되는 영향과 결과들의 발전에 대한 발표가 뒤를 이었다. 지난 세기 학자들 중 이렇게 다양한 분야에 지대한 자취를 남긴 사람이 있었던가? 그와 그의 업적에 대한 향연은 끝난 것이 아니라 세월이 흐를수록 더욱 커져가고 있다.

 

☞ DreamLove님의 추천 포스트

---

최종 확인 버전: 2014-03-11 18:51:02

• 관련 항목 : 수학 관련 정보
  

Incompleteness Theorems
쿠르트 괴델이 20세기 초반에 증명해버린 정리, 불확정성과는 다르다 불확정성과는 박사논문이었다……. 일부 책에서는 "결정 불가능 정리"라고도 나오는데 불완전성 정리가 맞다.

Contents

1 정리

2 '참'과 '증명가능'과 '귀결'

3 증명

4 예시

5 반응과 이용

[edit]

1 정리 ¶

이 정리는 다음의 두 명제로 이루어져 있다.

정리1. 자연수의 사칙연산을 포함하는 어떠한 공리계도 무모순인 동시에 완전할 수 없다. 어떤 체계가 무모순이라면, 그 체계에는 참이면서도 증명할 수 없는 명제가 존재한다. 
정리2. 자연수의 사칙연산을 포함하는 어떠한 공리계가 무모순일 경우, 그 공리계는 자기 자신의 무모순에 대한 정리를 포함할 수 없다.

'완전하다'는 것은 논리학 용어로서, 증명 불가능한 것이 있으면 불완전하고 증명 불가능한 것이 없으면 완전한 것이다.

즉 불완전성 정리는

• 자연수의 사칙연산을 포함한 어떠한 공리계에 대해서
  
  
  • 첫째, 그 공리계 내부의 자료만으론 기계적인 유한한 절차로 참, 거짓을 결정/증명할 수 없는 명제가 반드시 있다. 그렇지 않으면 그 공리계에는 모순이 있다.
  • 둘째, 공리계 스스로 자신의 무모순성을 증명할 수 있다면, 그 공리계 내부에 모순이 있다.
    

라는 것으로 수학적으로는 모든 문제를 풀어내는 일반적이고 기계적인 절차란 있을 수 없다는 것을 암시한다.(논리학적으로는 명제논리체계 등 가능한 체계도 있다.)

간단히, 무모순인 공리계는 참인지 거짓인지 알 수없는 명제를 포함하며, 스스로 무모순이라는걸 증명할 수도 없다.

논리학의 완전성 정리와 수학에서의 불완전성 정리를 함께 기억하는 사람들이 많은데, 괴델은 완전성 정리를 1929년, 23세때 박사논문으로 증명했고, 불완정성 정리는 그 2년후 25세때 증명하였다. 게다가, 대학때 입학한 과는 물리학과 였다. 덧붙여, 완전성 정리에 의해서 1차 술어 논리학[1]은 반드시 완전한 체계이다.

여기까지만 보면 괴델 혼자서 다한것같지만, 완전성 정리 및 불완전성 정리의 밑밥은 겐첸이 다 깔아놨고, 괴델은 가장 돋보이는 두가지 정리만 가져간것이라 보면 된다. 그리고, 무엇보다 겐첸은 힐베르트쪽에 붙어 불완전성보다 완전성을 증명하는데 촛점을 두었기때문에사람은 그래서 줄을 잘서야 한다. 겐첸은 결국 사칙연산 체계의 무모순성을 증명했지만, 사칙연산 체계를 넘어섰기때문에, 공리계 스스로 무모순을 증명한게 아니라 큰 의미를 갖지 못한 것일뿐이다. 다만, 그 사칙연산 체계를 넘어선 부분이 매우 작기때문에 Bernays 의 경우 처음 겐첸의 증명을 보고 정말 무모순성이 증명된줄 알았다고 한다. 그리고, 겐첸의 증명은 그 이상으로 많은것을 포함하고 있었기때문에 오늘날 증명이론에서도 중요하게 취급되고 있다.

완전성 정리와 불완전성 정리는 일반 스탠다드 classical logic 뿐 아니라, intuitionistic logic, minimal logic 등의 논스탠다드 논리체계에도 적용된다. 이 두가지뿐 아니라, 증명과정중 사용한 primitive recursive function 은 컴퓨터 과학을 탄생시키는 계기가 되기도 하였다. 하지만, 괴델은 이것을 실제 계산기와 같은 기계쪽에 응용할 생각은 하지 않았고관념적인것만 취급하는건가 후에 튜링이 primitive recursive function 을 보다 기계친화적인 튜링머신으로 바꾸어 표현하면서 컴퓨터의 아버지라는 이름은 튜링이 가져가게 되었다. 후에 클레이니가 여기에 mu-operator 를 추가하여 class of recursive functions 으로 진화시킨다. 그외에도 lambda calculus, unlimited register machine(URM), while-programming 등과 같은 여러가지 다른 공리계들이 존재한다. 서로 다른 수학자들에게서 독립적으로 서로 다른 방식으로 표현된 공리체계인데도 모두 같은 구조이다.[2]

증명에 대한 기계적인 절차를 제공할 수 있는 체계도 있다. 문장 논리에서는 반드시 그 논리 체계의 어떤 문장이라도 타당한지 타당한지 않은지를 검사할 수 있는 방법이 있으며(진리표 방법), 1차 술어 논리에서는 그 문장이 타당하다면 반드시 그것을 도출할 수 있는 방법이 존재한다.(귀류법을 응용한 방법이다.) 그리고 이 방법을 통해서 그 논리 체계가 완전함을 밝힐 수도 있다고 한다.(이것 역시 위에 나온 논리학의 완전성 정리로 괴델이 증명하였다.) 핵심은 수학의 경우에는 완전하다는 것에 대한 증명을 그 체계 자체에서 증명될 수 없다는 것이다. 그보다 상위 체계를 동원한다면 가능할 수 있는 것. 게르하르트 겐첸은 유한한 기계적 절차가 아닌 초한귀납법이라는 방법을 동원해서 수체계의 무모순성 증명을 증명하기도 했다.

그냥 관련된 이야기를 공부하고 있으면 세상엔 천재가 있음을 확인하게 된다.

읽어보면 좋은 책으로 <괴델,에셔,바흐>, <불완전성> 등이 있다.

[edit]

2 '참'과 '증명가능'과 '귀결' ¶

비전공자는 '참', '증명 가능', '증명 불가능', '독립성', '귀결' 등에 대하여 오해하기 쉽다. 그 대표적인 예시가 바로 엔하위키의 이 항목에 있던 다음과 같은 문단들이다:

[불완전성 정리에서 말하는 '참이라고도 거짓이라고도 증명할 수 없는 명제'는 증명도 반증도 불가능 하므로 참으로 간주하든 거짓으로 간주하든 자유다. 따라서, 현대수학은 증명불가능한 문제가 발생하면, 참 거짓을 따지기보다는 '어떤 공리를 추가하면 증명이 되고 어떤공리를 추가하면 반증이 되는가'식으로 흘러간다. ]

['참'과 '증명가능'은 완전히 다른 개념으로, 증명도 반증도 불가능하다고 하여 그 명제를 참으로 간주하든 거짓으로 간주하든 자유라는 말은 틀렸다. 어떤 명제의 참/거짓 여부는 그것의 증명/반증가능성과 관계가 없기 때문이다. ('참'의 정의는 다음과 같다: 명제 A가 참이다 = 공리들을 만족시키는 모든 모델에서 명제 A가 받아들여진다. = 명제 A를 부정했을때 공리들과 모순을 일으킨다.)]

먼저 입장을 명확히 하자. 여기서는 수리논리학, 그 중에서도 잘 사용되는 일차술어논리에서의 경우를 설명하도록 하겠다.(그 외의 논리에서는 다를 수도 있다. 명확하지 않음.)

먼저, φ가 명제의 집합 Γ의 귀결(logical consequence)이라는 것은 명제의 집합 Γ의 모든 명제를 만족시키는 임의의 모델에서 φ가 만족된다는 것을 의미한다. 또한 φ가 명제의 집합 Γ로부터 증명가능하다는 것은 Γ의 명제를 이용하는 기계적이고 유한한 절차만으로 φ를 산출할 수 있다는 것을 의미한다. 여기서 Γ 자체는 무한히 많은 명제들의 집합이라도, φ를 산출하는 데 실제로 사용된 Γ의 명제는 유한한 수이어야 한다.

그리고, 일차술어논리에 관한 세 가지 정리가 있다. 먼저 compactness theorem은 위상수학의 compact 개념을 적용한 것으로, φ가 명제의 집합 Γ의 귀결이면, 명제들의 유한집합 Γ'이 존재해서 "Γ'의 명제는 Γ의 명제이고, 즉 Γ'가 Γ에 포함되고, φ가 Γ'의 귀결이다" 가 성립한다는 것이다.

다음으로 completeness theorem(완전성 정리)과 soundness theorem(건전성 정리)에 의하여, φ가 명제의 집합 Γ의 귀결이라는 것과 φ가 명제의 집합 Γ로부터 증명가능하다는 것은 동치이다.[3]

또한, 제1불완전성 정리는 '참인 명제이지만, 그 긍정이 증명가능하지 않고 부정이 증명가능하지 않은 그런 명제가 있다' 쪽에 가깝다. 그리고 명제의 집합 Γ으로부터 φ도 notφ도 증명가능하지 않으면 φ는 Γ에 독립적이다고 말한다. 여기서 '참이지만 증명가능하지 않다'는 무슨 뜻인가? 이는 이렇게 생각할 수 있다. 아래에서 간략히 제시되겠지만 괴델의 아이디어는 증명가능성을 정수론의 개념으로 convert하는 것이다. 이는 이론체계 바깥에서 이루어지는 일이다. 이것이 잘 들여다보이는 바깥에서 볼 때, 그 convert 과정상 참일 수밖에 없는 문장이 있는데, 그것을 안에서 보면, 즉 그 이론체계 자체만으로는 긍정의 증명도 부정의 증명도 불가능하다는 것이다.

따라서, 위에서 []로 묶어 예시로 든 첫 번째 문단에서 '불완전성 정리의 조건을 만족하는 어떤 공리계에 대해서도 그에 독립인 명제가 존재한다'고 한 부분은 맞지만, 그렇다고 해서 참과 거짓을 엿장수 마음대로 정의할 수 있다는 것은 아니다. 바로 위에서 언급한 증명 과정상의 논의 외에도 수학과 수리철학 등에서의 여러 가지 복잡한 논의가 '참'에 얽혀 있다.

[]로 묶어 예시로 든 두 번째 문단에서 참과 증명가능을 구분하는 부분은 맞지만, 참과 귀결을 구분하지 않고 있는 부분은 맞지 않다. 일차술어논리에서 귀결과 증명가능은 동치이므로, 앞뒤가 맞지 않게 되기 때문이다.

정리하면, 참≠귀결=증명가능 이고, 괴델의 불완전성 정리는 어떤 공리계가 특정한 조건을 만족시키기만 하면, 명제 G가 존재해서 괴델의 불완전성 정리의 증명 과정에 의해 G가 참이라는 것을 알 수 있으면서 G의 긍정과 부정 어느 쪽도 그 공리계 내에서 증명가능하지 않다는 것이다. 괴델 이전에는 참과 증명가능을 잘 구분하지 않았기에 공리계를 적절하게 만들어 주면 참=증명가능 이고 긍정과 부정 한쪽만이 증명이 가능하지 않을까 생각하기도 했었는데(힐베르트 등) 괴델의 불완전성 정리 이후 그럴 수는 없고 참과 증명가능은 다르다는 것이 제기된 것이다.

연속체 가설 등의 명제들은 그 명제의 긍정과 부정 어느 쪽도 흔히 사용되는 공리계로부터 증명가능하지 않은 명제들이다.

[edit]

3 증명 ¶

구체적인 증명 없이 논리 구조와 아이디어만을 다룬다.

괴델의 첫 번째 정리를 증명하기 위해서는 '명제'를 숫자, 즉 자연수로 표현하는 굉장히 독특하고 기발한 방법을 사용했다.(사실, 명제가 구성되는 구조는 자연수와 유사하기때문에 수학적으로 보면 사실상 거의 같다. ] 이 방법(알고리듬)은 괴델의 이름을 따서 Goedelization 이라 칭하기도 한다. [4] 예를 들어,

')'→1,
'('→2,
'0'→3,
'1'→4,
'+'→5,
'='→6,...

이런 식으로 바꾸는 일반적인 법칙[5]을 제시하면 모든 (계산)명제는 숫자로 바꿀 수 있다. 예를 들어 방금 제시한 법칙으로 '1+0=1'을 쓰면 45364이란 숫자로 변한다.[6] 이 숫자를 괴델수Godel Number라고 하고, 괴델수는 당연히 원래의 명제와 일대일대응된다.[7]

이 방법을 응용하면, 명제와 명제와의 관계도 결국 '수와 수의 관계(연산)'가 되어버리므로 다시 숫자로 바꿀 수 있다(!) '참이면서 증명불가능한 명제가 있다'는게 첫번째 괴델의 정리는 대충 다음과 같은 명제를 이용한다.

"이 명제는 증명 가능하지 않다."[8][9]

이 문장은 1) 거짓이거나 2) 참이고 증명 가능하거나 3) 참이지만 증명 가능하지 않거나 셋 중 하나이다. 그런데 1) 거짓이라면 참이라고 증명이 가능해야 하므로 모순이다. 또한 2) 참이고 증명이 가능하다면 거짓이 되어 모순이 된다. 즉 이 문장은 3) 참이지만 증명 불가능해야 하는 것이다. 더 이상의 자세한 설명은 생략한다.

쉽게말해 명제를 적절하게 자연수로 바꿀 수 있고 따라서 "이 명제는 증명가능하지 않다."라는 명제를 자연수로 바꿔서 끼워넣으면 사칙연산(논리)에 따라 거짓말쟁이 역설이 일어나 공리계 내부에서 모순이 생긴다 것.

불완전성 정리에 사용된 거짓말쟁이 역설은 귀류법에 불과한데, 여기에 너무 치중해서 불완전성 정리의 핵심이자 그것이 기발한 이유인 증명이란 '객체'를 사칙연산 체계로 코딩하는 것, 그리고 거기서 computability를 이용하는 것을 간과하는 경우가 있다. 사실 불완전성 정리에서 사용된 귀류법 자체는 수학 증명에서 매우 흔히 사용되는 방법이라, 그다지 신기할것도 없다.

두번째 괴델의 정리는 앞서 만든 '참이면서 증명불가능한 명제'와 (가정한)'모순이 없이 스스로를 증명할 수 있는 이론체계'와의 관계를 (복잡하지만) 이용해서 무모순성을 스스로 증명할 수 없다는 것을 증명한 것이다.

괴델은 당시 w-consistency 을 전제하고 증명했는데, 후에 Rosser 는 이 조건 없이 증명을 해보여, 괴델-로서 정리라고 하는사람도 있다.

[edit]

4 예시 ¶

• 집합론 : ZFC[10]에서 선택공리(Axiom of Choice)[11]자신과 이를 이용해 증명한 정리들은 무모순하지만 다른 공리를 이용해서 참인지 거짓인지 증명할 수 없다.
  
• 연속체 가설[12] : 모든 무한집합의 원소수(기수)는 '알레프_n' 꼴로 표현 할 수 있다 여기서 알레프_1=2^(알레프_0)이 성립하겠느냐는 것이 연속체 가설이고, 일반화된 것은 알레프_(λ+1)=2^(알레프_λ)이 성립하지 않을까 하는 일반연속체가설. .[13]
  
• Word problem for groups[14]
  
• torsion-free, total separable group 은 free 인가[15]
  

[edit]

5 반응과 이용 ¶

이 정리 하나로 힐베르트와 프레게가 만들어나가던 "완전한 수학체계에 대한 꿈"이 박살났다.

괴델이 이것을 증명하기 20여년 전부터 힐베르트는 "모든 명제가 공리계로부터 증명 가능한 완전한 수학체계"라는 꿈을 가지고 있었다. 힐베르트는 이것을 위해 수학의 난제들을 하나하나 정리했고 프레게는 "수"와 "군"에 관한, 공리계의 기초를 닦아나가며 꿈을 키웠으나, 이 완전한 수학체계라는 것이 보시다시피 불완전성 제 1 정리와 완전히 반대되는 것이다. 즉 힐베르트가 꿈꾸던 수학체계는 완전히 박살나버렸다. 그래도 힐베르트 및 수학자들은 "그래도 저런 건 극소수고 중요한 정리들은 안 그럴거야"하면서 간신히 버텼으나 1963년에 힐베르트 자신이 가장 중요한 23개 수학문제 중에 제 1로 올려놓은 연속체 가설이 여기 포함됨이 증명되어 결국 완전한 수학체계의 꿈은 박살나버렸다.

당시에는 증명이 난해하다기보다는, 논리체계를 '이용하는' 수학이 그런 논리체계 자체를 수학적 대상으로 환원하여 연구한다는 부분을 잘 이해하지 못하여 대부분의 비수학자들은 그저 논리와 이성으로 이 세상을 완전히 설명할 수는 없다는 정도로 받아들일 수도 있을 것 같다, 는 식으로 이해했고, 지금도 비전공자들은 막연히 그정도로만 이해한다.[16]

철학자들 역시 예외가 아니어서, 철학적으로는 우리가 진리에 결코 도달할 수 없다는 뜻으로 해석되기도 한다. 몽테뉴, 니체가 했던 주장의 개정판인 셈이다. 이것도 물론 불완전성을 이해해서 확장했다기보다는 그냥 좋은 떡밥(같은 예로는 상대성이론, 양자역학)을 물었을 뿐이다. 불완정성 정리를 이용해서 개드립을 치던 신좌파 철학자들은 나중에 앨런 소칼에게 걸려서 박살이 났다. 원래 진리에 결코 도달할 수 없다는 주장의 기원은 소피스트가 자기네끼리 투닥투닥하던 시절까지 거슬러 올라간다.

문학에서는 어쨌거나 뜻의 난해함과 불완전성이라는 단어가 주는 포스트모던적인 강렬함 덕분에 억지를 진실로 진실을 억지로도 재정리 할 수 있는 논리체계라고 오해를 받는데, 괴델의 정리는 '참으로 증명된 정리'의 존재를 부정하지도 않고, 참인 명제를 거짓이라고 선언하지도 않는다.

SF에서 막판반전 혹은 도입부의 떡밥 강화용으로 사용된 적이 있고 80년대 후반, 동인 소설팀인 미도리쿠로시로의 시로쿠로미도리란 소설에서 주요 주제로 사용되었으나 반전을 반전으로 덮어 버리는 것을 반복하는 따라가기 어려운 글들이 되어버렸기에 주제로 내세우면 떡밥만 가득한 이상한 글이 되어서 대개의 경우 소리소문 없이 파묻혀 버렸다.
스즈미야 하루히의 우울 4권에서 언급되었으나 깊게 파들어가면 하나의 실수로 개피본단 것을 알고 슬쩍 떡밥 강화에쓰고 묻혔다..

모순성과 모든 것이 증명된다에 관한 논의는 프레게의 논리학 체계에서 나오는 '러셀의 역설'과 관련된 떡밥 같은데 러셀의 역설은 일반적인 논리 체계에서 적용되지 않는다. [17] 모순에서 모든 것이 증명된다는 것은 중세 때에 발견된 EFQ(Ex Falso Quodlibet, 둔스 스코투스의 정리)로, [18] 이것도 정확히는 '모든 것이 참으로 증명된다'는 의미라고 하는 것이 정확하겠다.

조금 더 일찍 나온 불확정성 원리가 주는, 세상은 확률론적으로 이루어져 '참과 동시에 거짓이다'라는 식의 오해가 쓰기 더 편리하기 때문에 더 이상은 등장하지 않을 듯 하다.

불완전성 정리를 주제로 한 단편 소설을 하나 쓸바에 들개를 훈련시켜 미국 대통령을 암살하는 일이 쉽다는 말도 있다.

사실 중세 및 근대초기, 오일러-가우스 시절까지의 수학에서는 지금의 고교수학 같이 단순히 주어진 수식의 연산정도만이 관심사였고, 해당 '체계' 및 '시스템 자체'의 엄밀함에 신경쓰기 시작한것은 코시라는 수학자가 등장한 이후부터였다.[19] 그러나 수학의 전체적인 시스템을 엄밀하게 증명하는 과정에서 제대로 좋은 결과를 보여준적은 거의 없다. 갈루아는 5차 이상의 방정식의 해를 구하는 공식은 없다는 결론을 내었고, 측도론에서는 실수공간의 임의의 부분집합의 넓이를 구하는 함수는 존재하지 않음을 보인데 더해서, 바나흐-타르스키 패러독스에서는 선택공리를 이용해 순수하게 자르기와 공간이동만의 방법을 사용해서 실수공간의 임의의 부피를 가진 공 여러개를 모두 같은 부피로 만들 수 있음을 보이기까지 한다.[20][21]

괴델의 불완전성 정리 역시 이 연장선상에서 수학 그 자체의 불완정성을 보인것이다. 현대수학은 매우 확고한 기초를 가진듯 보이지만, 사실 내부사정을 조금 들여다보면 이래저래 '의미적'으로도 위의 바나흐-타르스키 패러독스같은 여러가지 역설이 존재하기때문에 공격받는부분이 많고, 그외에도 철학적으로 비구성적 오브젝트를 허용한데 대한 입장차이등으로 인하여 공격받는 부분이 많아 '물 바깥에서 보기엔 우아하고 아름답지만, 안에서는 열심히 다리를 허우적대는 백조'와 같은 모양새를 띄고 있다.

골드바흐의 추측과 얽혀서 "어쩌면 골드바흐의 추측도 저 "참이면서도 증명할 수 없는 명제"(참 거짓을 증명 할 수 없는 문제)가 아닐까?" 하는 떡밥을 써먹은 소설 <사람들이 모두 미쳤다고 말한 외로운 수학 천재 이야기>가 있다. 아직까지 증명도 반증도 안되니 참으로 간주하는 것. 페르마의 대정리도 증명되기 전에는 비슷한 의심을 하는 사람들이 있었다.

나가토 유키는 이 말을 차용해서 비슷한 말을 남겼다.

----

• [1] 양화사가 술어에는 허용되지 않고 오로지 주어에만 허용되는 논리체계
• [2] 이 공리체계들은 알고리즘을 표현하는 공리체계인데, 이것들이 모두 같은 구조를 띄고 있다는 점에서나온게 "이 공리계에서 나온 알고리즘이 곧 모든 알고리즘"이라고 간주하는 주장이 그 유명한 Church's thesis이다.(알고리즘이 수학적 혹은 논리적으로 명확히 정의된 개념이 아니라서 이 공리체계들이 모든 알고리즘을 포함하는지는 증명 불가능하다.)Chruch's thesis는 사실 수학보다 철학이나 물리학, 인공지능 분야에서 '인간의 사고를 알고리즘으로 표현이 가능한가'와 같은 문제와 관련이 깊다.(사실 집합론과 category theory 정도를 제외한 대부분의 수리논리학 분야는 일반적으로 대학 수학과와는 큰 관련이 없다.)
• [3] 완전성 정리와 건전성 정리와 위의 정의로부터 compactness theorem이 증명되기도 한다.
• [4] 나중에 튜링Turing도 이 방법을 차용하여 튜링머신을 만들었다.
• [5] 정해져있지 않고 맘대로 정할 수 있다. 여담이지만 위키백과에서는 기초적인 10개의 '불변부호', 즉 (나 0, s같은 것들에 1~10을 정해놓고, 기타 나머지 경우에는 변수마다 종류를 나눠 n번째 종류의 k번째 변수에 해당하는 괴델 수를 (10 이후의 k번째 소수)^n으로 제시했다. 이렇게 하면 모든 수마다 절대로 지정된 수가 겹칠 일이 없다.
• [6] 엄밀히 따지자면 이렇게 했을 경우 10 이상의 숫자에 대응할 수가 없기 때문에 실제로는 저렇게 해당하는 숫자를 나열하지는 않고 각각 2, 3, 5, 7...으로 소수의 순서를 정한 다음 각각의 수를 순서대로 각 소수의 지수로 놓는다. 이렇게 하면 1+0=1이라는 명제의 괴델 수는 837134518374000이 된다.(2^4×3^5×5^3×7^6×11^4) 본문의 예는 이해를 쉽기 위해 든 간단한 아이디어만을 서술했기 때문에 이 내용을 각주로 뺀다.
• [7] 괴델,에셔,바흐에서는 MU라는 연습문제 비슷한 퀴즈를 주는데 이걸 위해서 시키는 것이다.
• [8] "이 문장은 거짓이다"와 비슷해 보이지만 이 명제는 모순이 아니고, 위 표현법으로 나타낼 수 있다. "이 문장은 거짓이다" 라는 문장은 위 표현법으로 나타낼 수 없음이 증명되어 있다.
• [9] 참고로 실제로 괴델의 증명에서 사용된 엄밀한 식은 ∀x ~Dem(x,sub(n,k,n))이다. 여기에서 Dem(x,y)란 괴델수가 x인 명제가 괴델수가 y인 명제를 증명한다는 뜻이며, sub(n,y,n)은 괴델수가 n인 식에서 괴델수가 k인 변수를 전부 괴델수가 n인 식으로 치환한다는 뜻이다. 이 식은 결국 자기 자신에 대해 무한 반복이 되는 명제이므로 '이 문장 자신'을 뜻한다. 즉 이 명제의 뜻은 '괴델수가 몇인 명제이든 이 명제를 증명할 수 없다'는 뜻이다. 즉 '이 명제는 증명 가능하지 않다'와 동치이다.
• [10] Zermelo-Fraenkel Set Theory + Axiom of Choice
• [11] 여러 개의 집합이 있을 때, 각각의 집합에 그 집합의 원소를 하나씩 대응시키는 함수가 엄밀하게 따져도 가능하고 존재한다는 공리. 여러 개의 집합이라고 했는데, 유한 개의 집합이 있는 경우와 무한 개의 집합이 있는 경우 둘 다 허용하는데, 유한 개의 집합의 경우는 이 공리가 없어도 가능은 하다. 결론적으로 바로 앞의 함수를 이용하면 여러 개의 집합에서 하나씩 원소를 뽑아서 집합을 만들 수 있게 된다.
• [12] 선택공리와 연속체 가설이 증명 불가능하다는 것은 모두 폴 코헨(Paul Cohen)이 증명했다.
• [13] 알레프_0=자연수 집합의 기수이고, 그 바로 다음으로 많은 것이 알레프_1, 그 바로 다음으로 많은 것이 알레프_2, ... 으로 이어진다. 2^(알레프-λ)는 알레프_λ만큼의 원소를 가지는 집합의 멱집합의 원소수. 자세한 것은 연속체 가설과 초한기수 문서 참조.
• [14] 공리계에 관한 내용은 아니지만, Undecidability 에 관한 문제라, 불완전성 정리와 가까운 문제라 볼 수 있다. 유한집합인 임의의 알파벳 A 의 문자로 생성된 group G 가 있다고 하자. 역시 A 의 문자들로 구성된 임의의 word 2개를 만들어, 그것이 G 에서 같은 원소인지 아닌지 구분하는 알고리듬이 존재하는가 하는 문제인데, Higman 에 의하여 불가능하다고 증명되었다.
• [15] ZFC 에서 증명도 반증도 불가능하다. ZFC에 V=L(이 역시 괴델이 제시한것으로, 괴델 공리라고도 불린다.) 공리를 추가하면 free 가 맞고, MA(Martin's axiom) 와 연속체가설의 부정을 추가하면 free 가 아니다.
• [16] 그러나, 사실 그렇게 난해하지만은 않으며, 이해하기 위해 필요한 사전지식도 매우 적은편이다. 실제로, 복잡한 정도로만 따지자면 완전성 정리가 더 복잡하다. 관련학과를 들어가면 대학원도 아니고 학부때 수리논리를 택하면 배울 수 있다. 사실, 수리논리 전공에서 불완전성 정리는 입문정도에 해당한다.
• [17] 정의 대신에 공리계를 이용한다던가 해서 모순을 일으키는 대상을 집합으로 보지 않는다.
• [18] 직관주의 논리체계에서는 이것이 연역되지 않기때문에 공리로 사용하며, 스탠다드 논리체계에서는 다른 공리들에 의해 연역된다.
• [19] 그래서, 오일러 이후로 수학은 끝난줄 알았는데 가우스가 등장했고, 오일러-가우스 이후로 수학이 끝난줄 알았는데 코시가 등장했다라는 말도 있다.
• [20] 간단히 말하면 부피 1m³ 의 냉장고에 100m³ 의 코끼리 100마리를 따로 압축하거나 하지 않은채 순수하게 쪼개서 차곡차곡 개어넣을 수 있다는 소리다. 비밀은 쪼개는 방법에 있다. 이 쪼개는 방식은 무한대의 횟수로 쪼개 나가야 하기 때문에 현실에서 이를 실험하기는 불가능한 것이다.
• [21] 여담으로 리처드 파인만은 자신의 공감각을 이용하여 수학과 동창들과 자주 논쟁을 벌였다고 하는데, 하루는 오렌지 하나를 쪼개고 이동시켜서 오렌지 두개를 만들 수 있냐는 질문을 받았고, 가능하다는 수학과 동창에게 한 반박이 이거다. "원자보다 작게 쪼갠 오렌지가 오렌지냐?" <- 이는 말이 되지 않는 소리이다. 그가 한 말은 원자보다 작게 쪼개는 것은 불가능하므로 불가능하다는 이야기였다.